To understand the statistics published by the
Internet Routing Entropy Monitor,
you may need to make yourself familiar with some essentials on IP addressing
and routing. The below short intro will hopefully prove useful in this.
Henceforth, we shall concentrate on IP version 4 exclusively, even though
the theory is basically the same for IP version 6 as well.
IP addressing
As of version 4 of IP, hosts, or more precisely, the individual interfaces
by which the hosts attach to the Internet are identified by 32 bit numbers,
the so called IP addresses. For instance, the IP address of the server that
hosts the
Internet Routing Entropy Monitor
is given as follows in some
popular notations:
| dotted-decimal |
152.66.244.224 |
| 32 bit unsigned integer |
2554524896 |
| 32 bit binary |
10011000 01000010 11110100 11100000 |
Packets traveling on the Internet all carry the IP address of the host they
are destined to, which is then used by Internet routers to forward the
packets towards the intended destination. To do so, routers maintain a giant
database, called the forwarding table, or
Forwarding Information Base (FIB),
which for each destination address tells to which next-hop router a packet
with that address should be forwarded. This way, packets travel from the
originating host to the destination host hop-by-hop.
Since there are more than 4 billion IP addresses, it would
not be too practical for the FIB to maintain a separate entry
for each and every IP address. Internet routing applies a
clever trick to sidestep this problem, the Classless Inter-domain Routing
(CIDR) scheme. In CIDR, IP hosts are collected, on an
administrative or geographical basis, into groups called
subnets. Each IP host's
address within a subnet begins with the same initial binary
prefix, making it possible for the rest of the Internet to
refer to any host within the subnet using that prefix. For
instance, the server that hosts the Internet Routing Entropy Monitor
resides within the BMENET
subnet, identified by the following prefix:
| dotted-decimal |
152.66.0.0/16 |
| 32 bit binary |
10011000 01000010 00000000 00000000 |
This essentially means that any host whose IP address begins with the 16 bit
binary prefix 10011000 01000010, or matches the
wild card 152.66.0.0 on the first 16 bits,
resides within BMENET. This facilitates to refer
to all the possibly 216=65536 hosts within
BMENET with a single entry in the forwarding
tables of IP routers.
The FIB
Thanks to CIDR, it is enough for Internet routers' forwarding tables to
maintain a single entry for each subnet, with the semantics that any
packet with a destination address matching the IP prefix of the subnet
will be forwarded to the next-hop specified in the forwarding table for
that subnet.
Consider the simple excerpt from a real IPv4 FIB:
| IP prefix/prefix length |
Next-hop address |
| ... |
| 152.61.128.0/18 |
10.0.0.1 |
| 152.66.0.0/16 |
10.0.0.2 |
| 152.66.127.0/24 |
10.0.0.1 |
| ... |
The first entry in this FIB segment encodes the forwarding semantics that
any packet with a destination address within the prefix
152.61.128.0/18 (i.e., in the range
152.61.128.0 to
152.61.191.255) should be forwarded to the next-hop
whose IP address is 10.0.0.1.
Furthermore, packets destined to any host within
152.66.0.0/16 take the next-hop router
10.0.0.2. Observe how the clever trick of CIDR
hides the uninteresting internal details from the outside, providing just
enough information for the rest of the Internet to route
route precisely the required packets into the subnet, from
where it is the responsibility of the subnet's owner to
distribute them to the hosts.
The third entry, however, is a bit peculiar. In particular, it turns out
that the prefixes in the second and the third entries
overlap.
Therefore, for some IP addresses, like for instance
152.66.127.132, there are two matching entries in
the FIB, with two distinct next-hop addresses! In such cases, the longest
prefix match rule applies, dictating that the entry that matches on the
most bits (starting from the most significant bit) takes precedence.
Thusly, packets with the IP address 152.66.127.132
will be handled by the third entry as it matches on 24 bits instead of
only 16, and hence forwarded to the next-hop 10.0.0.1.
The longest prefix match, although increasing the FIB size with introducing
such "more-specifics" and also exacerbating FIB lookup substantially, is
extremely useful for network operators to fine-tune the way traffic
enters their subnet.
Observe that the FIB sample uses private IP addresses
(in the prefix 10.0.0.0/8) to encode next-hops.
This anonymization is applied to hide the exact internal forwarding policies
implemented by the FIB, in order to protect our data sources' privacy.
Note, however, that the mapping is consistent in that the same next-hop is
always mapped to the same private IP address, and hence next-hop distributions
are perfectly maintained. This next-hop anonymization technique is used all
over the
Internet Routing Entropy Monitor and it is
applied for all the FIB data sets available for download.
Prefix trees
Finding the longest matching prefix for a given IP address is not especially
easy. One reason is exactly the longest prefix match semantics itself,
while the other is that a full-fledged Internet FIB today,
CIDR addressing notwithstanding, contains well above 500 thousand entries
and counting (see the corresponding charts
below).
This essentially rules out the naive implementation,
one that would search through all the prefixes stored in the FIB one by one,
and calls for more sophisticated lookup schemes. The most common FIB data
structure is, correspondingly, the prefix tree
(or some variant of it).
Consider the FIB sample below.
| Prefix in dotted-decimal |
Next-hop address |
Prefix length |
Next-hop |
| 0.0.0.0 |
0 |
0 |
10.0.0.2 |
| 64.0.0.0 |
010 |
3 |
10.0.0.1 |
| 96.0.0.0 |
0110 |
4 |
10.0.0.2 |
| 128.0.0.0 |
100 |
3 |
10.0.0.1 |
| 160.0.0.0 |
1010 |
4 |
10.0.0.2 |
| 192.0.0.0 |
1100 |
4 |
10.0.0.2 |
| 228.0.0.0 |
111 |
3 |
10.0.0.2 |
| 244.0.0.0 |
1111 |
4 |
10.0.0.1 |
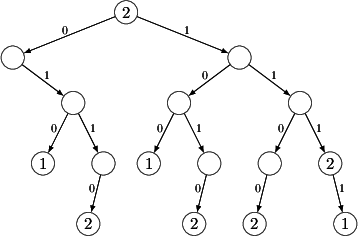
The prefix tree corresponding to this FIB takes the following form.
For brevity, in the above figure the next-hop IP addresses are substituted
with a single label corresponding to the last byte of the IP address.
Also take note of the first entry, 0.0.0.0/0.
This prefix matches every IP address, but any other prefix that happens to
match the address is more specific. Therefore, this entry is called the
"gateway of last resort" (or the default gateway):
if no entry matches a packet then forward the packet to the next-hop
10.0.0.2.
Here is how IP address lookup occurs using this prefix tree. Suppose that we
are given the IP address 245.124.32.17,
whose binary form is 11110101 01111100 00100000 00010001.
We take off from the root of the prefix tree
(i.e., the topmost node) and we note that this node contains the label
corresponding to the next-hop 10.0.0.2.
This means that the default
gateway matches our IP address, so we immediately have one candidate lookup
result. Our task is now to iteratively refine this match until we find the
most specific matching entry.\
The iteration starts with taking the first bit of the IP address. In this
case the first bit is 1, so we take the right
child of the root node along
the arc marked by the label 1. Should the first
bit be zero, we would have
stepped to the left instead of to the right. Since the right child node does
not contain a label no new matching FIB entry has been found, so we still go
with the default gateway. Next we take the second bit, which is again
1,
thus we again take the right exit and we follow this process recursively,
traversing the tree downwards until we end up in a node that
has no outgoing arc emanating from it marked with the
subsequent bit in the IP address (e.g., a leaf node that has
no children associated to it at all). In each step, we note the last label we have
found along the way as the most specific match. Hence, in the third step we
find the node label corresponding to the next-hop
10.0.0.2 (this
corresponds to the FIB entry 111/3 -> 10.0.0.2),
which is then overridden
in the last, fourth step when we find the leaf node with label
1 (FIB entry
1111/4 -> 10.0.0.1). We conclude that the best
match is the next-hop
10.0.0.1 and we terminate the process.
What is remarkable in the prefix tree data structure is that the above lookup
process is guaranteed to terminate in at most as many steps as there are bits
in the IP address (32 for IP version 4, and 128 for version 6), which is way
faster than tediously looping through all the FIB entries one by one. Adding
a new entry, or deleting or modifying an existing one, goes in the same
number of steps, making prefix trees extremely appealing for storing the
forwarding table in IP routers.
An information-theoretic view on IP FIBs
There has been an ongoing research effort for many years to reduce the memory
footprint of the above prefix tree data structure (or improve the lookup
speed further, for that matter). Easily, the smaller the FIB the more
entries can be squeezed into the limited memory of IP routers, letting the
Internet to scale to ever-more users and end-hosts. As such, the information
content of the FIB tells an interesting story about the
long-term scalability
perspectives of the Internet architecture. If the memory footprint were
large, or it were to skyrocket with every new prefix added, then this would
cast a very dark shadow over the future of the Internet, essentially
inhibiting it from scaling beyond a certain limit. The main purpose of
creating the Internet Routing Entropy Monitor
was to answer these
fundamental questions by observing the information content of several real IP
routers around the globe.
What remained to be done is to somehow define a metric that would
characterize the information content of a forwarding table. This metric is
loosely referred to as entropy in
information-theory.
Below, we attempt to define the FIB entropy in layman's terms.
For more in-depth coverage, consult the papers
[1], [2].
The leaf-pushed prefix tree
The first problem we face is that there are many equivalent ways to describe
the same forwarding semantics using prefix trees. That is, a prefix tree can
take many equivalent forms, each defining exactly the same packet forwarding
rules, and it is not especially easy to decide which one to choose to derive
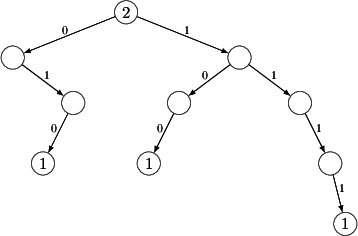
FIB entropy from. For instance, the below prefix tree is easily seen to
associate the exact same next-hop to each fully-specified IP address as the
original one, yet it is substantially smaller.
The trick here is that we are free to play around with more specifics,
opening the door to an assortment of semantically equivalent prefix tree
representations with highly different structure. What we need is a
"normalized" form for FIBs of some sort, one that would be the same for each
and every semantically equivalent FIB. Such a normalized form is the binary
leaf-pushed prefix tree.
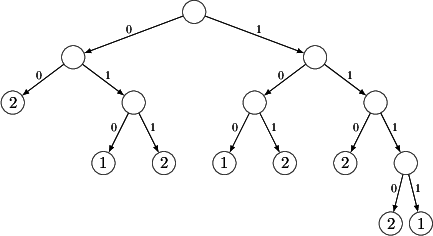
The idea is that we eliminate all less-specifics from the FIB, essentially
transforming the forwarding table into a minimal prefix-free form. Consider
the below leaf-pushed prefix tree for our running example.
One easily checks that, on the one hand, this form associates the exact same
next-hop to each address as the original one and, on the other hand, the
corresponding forwarding table (see below) has the property that no entry is
the prefix of another entry. It can be proved that, thanks to the prefix-free
property, the leaf-pushed prefix tree representation of the FIB is unique,
providing an excellent basis to derive FIB entropy from.
| Prefix in dotted-decimal |
Next-hop address |
Prefix length |
Next-hop |
| 0.0.0.0 |
00 |
2 |
10.0.0.2 |
| 64.0.0.0 |
010 |
3 |
10.0.0.1 |
| 96.0.0.0 |
011 |
3 |
10.0.0.2 |
| 128.0.0.0 |
100 |
3 |
10.0.0.1 |
| 160.0.0.0 |
101 |
3 |
10.0.0.2 |
| 192.0.0.0 |
110 |
3 |
10.0.0.2 |
| 228.0.0.0 |
1110 |
4 |
10.0.0.2 |
| 244.0.0.0 |
1111 |
4 |
10.0.0.1 |
The information-theoretic lower-bound
From this point, we are ready to cast the task to define the FIB entropy
notion using information-theoretical arguments. Let \(\Sigma\) denote the set
of next-hop IP addresses in the FIB, let \(n\) denote the number of leaf nodes in the
leaf-pushed tree, and let \(n_i\) denote the number of times next-hop \(i \in
\Sigma\) appears as a label for a leaf node in the leaf-pushed tree. Using
this notation, the relative frequency of next-hop \(i \in \Sigma\) appearing in
the leaf-pushed tree is \(p_i = \frac{n_i}{n}\).
The first notion of information content, called the information-theoretic
lower-bound, roughly corresponds to the number bits needed to assign
for each instance of leaf-pushed trees on \(n\) leaves a unique identifier and
using that identifier to refer to the FIB. In the case of IP FIBs, the
empirical information-theoretic lower bound is \(2n + n \log_2 |\Sigma|\)
bits, where \(n\) and \(\Sigma\) are as above. The (very simplified) explanation
is that we need at most \(2n\) bits to differentiate between any two unlabeled
binary trees on \(n\) leaves, to which the size of the string comprised by the
next-hop addresses written to the leaf nodes adds another \(n \log_2 |\Sigma|\)
bits. Note, however, that this simple formula provides only an approximation
to the information-theoretic lower-bound, which is, unfortunately, extremely
difficult to quantify precisely [1]. In fact, the real
metric is somewhat smaller, but the above estimate still proves very useful
in practice.
FIB entropy
The information-theoretic lower bound gives an estimate of the information
content of the FIB in the case when we know nothing about its internals,
i.e., if we took the FIB as essentially random. However, very often we have
more knowledge from a forwarding table and we can make use of this insight to
compress the FIB to below the information-theoretic lower bound.
For instance, we could make some statistics about the distribution of
next-hop labels in the leaf-pushed tree and then we could use the standard
trick of data compression to encode popular next-hops on only a few bits and
less popular ones on more bits. This way, whenever we encounter a popular
label we use fewer bits than a naive encoder would do, which greatly
compensates for the bits we waste when encoding less popular next-hops. This
is the idea behind many data
compression schemes, and this is also the way we associate an entropy
measure to IP FIBs.
Define the empirical Shannon-entropy of the
next-hop distribution in the leaf-pushed tree as
usual:
\begin{equation*}
H_0 = \sum_{i\in\Sigma} p_i \log_2\left( \frac1{p_i} \right) \enspace .
\end{equation*}
Note that the entropy of the next-hop distribution is guaranteed to be
smaller than the information-theoretic lower bound, that is, \(H_0 \le
\log_2 |\Sigma|\), with equality if and only if the next-hop distribution
\(p_i: i \in \Sigma\) is uniform. Hence, any encoder that attains the entropy
is guaranteed to compress below information-theoretic lower bound, unless the
input data is completely random.
Using this notation, the empirical FIB entropy bound
is \(2n + n H_0\) bits,
where again \(n\) is the number of leaf nodes in the normalized (leaf-pushed)
prefix tree for the FIB and \(p_i\) describes the relative frequency of
next-hop \(i \in \Sigma\) appearing as a next-hop label on the leaves. The
explanation in layman's terms is that we need roughly \(2n\) bits to encode the
tree, to which the next-hop string written to the leaves gives an extra \(n
H_0\) bits. Again, this is only a very simple conservative estimate of the
real-entropy (which would otherwise be next to impossible to compute
precisely), but even this crude estimate is already very useful in practice.
What the FIB entropy is NOT
Above all, it is not a metric on
compressibility. Or it is possible that it actually is, but
so far no one has actually proved this.
Let us dig a bit deeper. In standard information-theory, a very
important theoretical property of the entropy bound is that it
gives a good estimate on the minimum number of bits needed to
encode whatever data. For sequential data (like a string), it is
well-known that the entropy bound of \(nH_0\) bits provides an
absolute limit on the best possible lossless compression of that
data (at least, with a zero-order encoder). Unfortunately, this
argumentation does not quite bring over to IP FIBs, or at least we
still do not know whether it does. The reasons are multiple. First,
even the entropy bound of \(2n + n H_0\) bits is already a
(conservative) approximation and the real entropy bound should be
somewhat smaller. Second, we still do not know whether or not the
leaf-pushed prefix tree is a minimal data structure to encode the
subnetting hierarchy inherent to the IP address space, and it can
very well happen that other representations yield smaller entropy
bounds.
What the FIB entropy is
Still, the notion of FIB entropy presents a unique opportunity to
look into the very knowledge encoded in the Internet data plane, as
described below.
- Regularity: The FIB entropy bound of \(2n + n H_0\) bits is shaped by two
essential factors, namely, the number of leaves \(n\) of the leaf-pushed tree
and the Shannon-entropy \(H_0\) of the next-hop distribution. Interestingly,
there is an intricate interdependence between these two factors. Imagine
two FIBs containing identical number of entries, one FIB with a dominant
next-hop carrying most of the prefixes and the other FIB with roughly
uniform next-hop distribution. The first FIB's
next-hop distribution will be very biased (i.e.,
highly regular), reducing the leaf-pushed tree size \(n\)
and/or the Shannon-entropy \(H_0\), leading to a
small entropy bound. The other FIB, however, is of
maximal entropy, and thusly cannot be substantially
compressed beyond the information-theoretic
minimum. The Shannon-entropy of the next-hop
distribution is therefore a very good indicator of
the regularity hidden deep within the seemingly
complex forwarding rules implemented by an IP router.
It must be noted, though, that the entropy \(H_0\)
should always be viewed side-by-side with the size
parameter \(n\), or the entropy bound \(2n + n H_0\),
as in itself neither is decisive.
- Routing policies: The Shannon-entropy of an IP FIB presents a bird's-eye
view of the routing policy as implemented by an Internet router. If the
entropy is small then the next-hop distribution is highly biased,
indicating the presence of a dominating next-hop, say, a default route or a
primary provider. Interestingly, most of the FIBs we collect from vantage
points are of this type. If, on the other hand, the entropy is large, say,
close to the information-theoretic limit \(H_0 \approx \log_2 |\Sigma|\),
then each next-hop is likely to appear with equal probability for any
prefix. So far we have not seen any FIB of this type, but we know
theoretically that they should arise in reality. For instance, we would
expect such FIBs to show up at Internet eXchange Points (IXPs).
- Space upper bound: Even
though not a lower bound on
the amount of bits needed to encode a FIB, the FIB
entropy is still a very useful upper-bound on the space
requirements thereof, in that there are actual FIB
compressors that attain the \(2n + n H_0\) bits storage space
limit in practice [1], [2]. That means that we never need
more bits than the entropy bound (subject to smaller order
error terms), while we may very well get on with fewer bits
in some cases.
- Information content: It turns out that the entropy bound gives an
appealing way to characterize the amount of information present in the
FIB. The entropy bound of \(2n + n H_0\) bits simply means that a FIB
contains (at most) an equivalent of answering precisely \(2n + n H_0\) yes-or-no
questions. Easily, the latter is possible by storing \(2n + n H_0\) bits,
each one specifying the answer to one of the questions (say, 0 would mean
no and 1 would mean yes), and this simple argumentation supplies a
universal scheme to measure the information content encoded in an IP FIB.
- Complexity: The above universal interpretation of FIB information content
allows us to compare the complexity (in terms of the amount of information
stored) of an IP FIB to essentially any other data. For instance, we
see that a full-fledged IP FIB, containing more
than 500,000 entries, stores roughly 150-200 KBytes of information. This
is equivalent to a larger email message, a smaller PDF document, a low
resolution photo image, or roughly 600,000 characters of English text (the
equivalent of a small novel). And it is way smaller than any computer
encoded music file, photo of reasonable resolution, or most of the
executable files on your PC for that matter. It seems that IP packet
forwarding is not that difficult after all, despite that we are talking
about a world-wide network infrastructure connecting billions of hosts!
- Evolution: The evolution of FIB entropy, being
a metric of information complexity for IP forwarding, gives us
a glimpse into the very sustainability of Internet routing. It seems that
the entropy has been fairly constant throughout the last few months, or it
has changed very little over time. It would be tempting to arrive to the
reassuring conclusion that the long-term scalability perspectives of the
Internet routing ecosystem are pretty rosy. Nevertheless, it must be
mentioned that the sample size and the time frame described in the
statistics do not allow to make overall conclusions. For this,
we would need much more data!
- Faster lookups: As it
turns out, not just that the entropy gives a crude upper
bound on the number of bits we can compress an IP FIB down to
and that this bound is in fact attainable by real life FIB
encoders, but this comes without
sacrificing lookup performance is any ways whatsoever
[1]! In fact, IP lookups on the
compressed form are usually much faster than on the
uncompressed one, due to the improved cache-friendliness
caused by smaller memory footprint. This holds a great
potential for IP FIB compression.
Statistics
Here is a short recap on the most important statistics published at the
Internet Routing Entropy Monitor.
Click here for more
background on the data.
- Entropy (\(H_0\),
[bits]): The Shannon-entropy of
the next-hop distribution on the
leaf-pushed prefix tree. To obtain it, the raw FIB is converted into a
normalized leaf-pushed prefix tree and then the Shannon-entropy of the
resultant leaf-label distribution is computed.
- Number of raw FIB entries: The number of
entries in the original FIB, as
downloaded from the vantage point routers. Should be in the range of
several hundred thousands for full-BGP FIBs and several thousands for FIB
instances with a default gateway.
- Entropy bound (\(2n + nH_0\), [Kbytes]): The entropy
bound derived from the
leaf-pushed prefix tree representation of the FIB. The raw FIB is
converted into a normalized leaf-pushed prefix tree form and then the
entropy bound is computed from the number of leaf nodes \(n\) within this
form and \(H_0\), the Shannon-entropy as above.
- Number of next-hops: As the name suggests,
the number of individual
next-hop IP addresses as appearing in the FIB.
- Next-hop CDF: The cumulative distribution
function of next-hop label
distribution within the FIB. The FIB is first converted into a normalized
leaf-pushed form and the relative frequency of each next-hop address is
calculated. For this, the number of times \(n_i\) for each next-hop \(i \in
\Sigma\) appearing in the leaf-pushed prefix tree as a leaf label is
computed. Then, next-hops are arranged into an ascending order of
popularity and the cumulative distribution function is depicted on a
log-log scale that for each next-hop gives how many times this next-hop and
all the less popular next-hops appear in the FIB.
The below table shows the statistics on the FIBs collected from the individual vantage
point routers. Click on the '+' sign to expand the per-FIB statistics, which
can then be collapsed again by clicking on the '-' sign.
![[+]](images/expand.png) Background
Background

![[+]](images/expand.png) Atlanta
Atlanta
![[+]](images/expand.png) Chicago
Chicago
![[+]](images/expand.png) Cleveland
Cleveland
![[+]](images/expand.png) Houston
Houston
![[+]](images/expand.png) KansasCity
KansasCity
![[+]](images/expand.png) LosAngeles
LosAngeles
![[+]](images/expand.png) NewYork
NewYork
![[+]](images/expand.png) SaltLakeCity
SaltLakeCity
![[+]](images/expand.png) Seattle
Seattle
![[+]](images/expand.png) Washington
Washington
![[+]](images/expand.png) hbone_bme
hbone_bme
![[+]](images/expand.png) hbone_debrecen
hbone_debrecen
![[+]](images/expand.png) hbone_miskolc
hbone_miskolc
![[+]](images/expand.png) hbone_pecs
hbone_pecs
![[+]](images/expand.png) hbone_sopron
hbone_sopron
![[+]](images/expand.png) hbone_szeged
hbone_szeged
![[+]](images/expand.png) hbone_szolnok
hbone_szolnok
![[+]](images/expand.png) hbone_veszprem
hbone_veszprem
![[+]](images/expand.png) hbone_vh1
hbone_vh1
![[+]](images/expand.png) hbone_vh2
hbone_vh2